Tirolesa de corda: princípios de funcionamento, instalação e dimensionamento
Curta história...
Curta história...
Alguns afirmam que o primeiro construtor de uma autêntica tirolesa foi o holandês Adam Wybe em 1644, era para facilitar a construção de uma fortaleza em Danzig na Polonia, ele instalou uma corda de cânhamo em movimento contínuo com vagões de transporte, uma espécie de teleférico. No entanto, a divulgação dos teleféricos na Europa começou a partir da segunda metade do século XIX. Em 1868, o engenheiro inglês ch. Hodgson, inscreveu a patente de um sistema com os vagões apoiados por uma corda metálica (cabo de aço); em 1873 os engenheiros alemães Kramer, Bleichert e Otto mudaram este sistema por um com 3 cordas e no mesmo ano, o Von Dücker construiu em Metz uma tirolesa de movimento contínuo com três cordas e com uma ancoragem automática entre os vagões e as cordas. Anos depois, houve uma grande mudança e desenvolvimento na Europa dos teleféricos, principalmente para o transporte de materiais em minas e no ambiente montanhoso com difícil topografia.
(Treccani)

Tirolesa, além de ser utilizada para o transporte das coisas ou em alguns casos de pessoas nas montanhas, também se aplica durante as operações de acesso e resgate nos trabalhos verticais; graças a ela pode-se chegar a áreas naturais dificilmente acessíveis ( Paredes rochosas, cânions, taludes, etc. ) e artificiais (Torres, pontes, estruturas arquitetônicas complexas, etc. ).
O que é uma Tirolesa?
O cabo é uma catenária, uma vez que, por definição: todos os fios, cabos e também as cadeias e em geral qualquer objeto flexível, homogêneo e não extensível de um certo comprimento fixo em dois extremos, está sujeito devido à força da gravidade para o seu próprio peso e portanto, assume uma configuração de equilíbrio tal que cada seção do mesmo é enfatizada pela tração; o mesmo acontece se, além disso, também se houver cargas externas concentradas ou distribuídas ao longo de todo o seu comprimento.
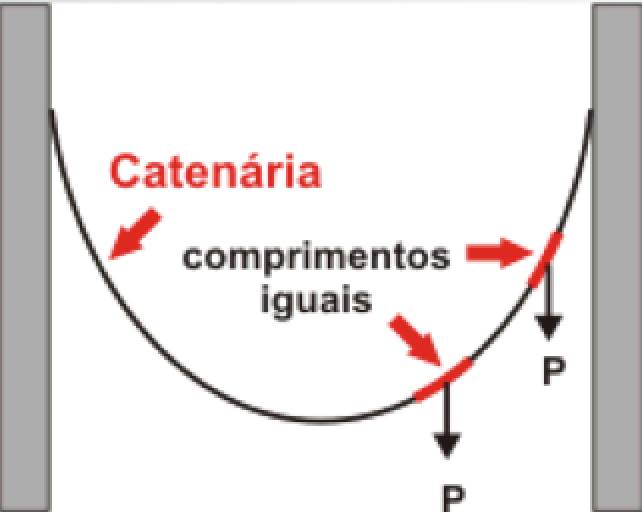 “Qual é a condição para que o cabo tenha a forma de uma catenária?
“Qual é a condição para que o cabo tenha a forma de uma catenária?O cabo assume a forma de uma curva denominada de catenária quando ele está submetido apenas ao seu próprio peso.
Catenária >>> carga uniformemente distribuída ao longo do cabo.
Ela se expressa com o cosseno hiperbólico. Em muitos casos, no entanto, é feita referência à parábola (muito semelhante em natureza à catenária) para as operações de dimensionamento e a identificação do equilíbrio das cordas em geral, uma vez que a última é mais fácil de usar.
Abaixo estão ilustrados três esquemas muito simplificados, que podem ajudar na compreensão das forças envolvidas no "sistema de tirolesa".
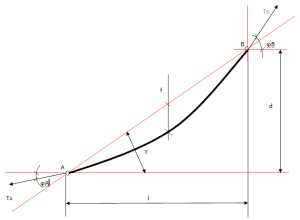
figura 1 - Tirolesa Inclinada
-
A, B : extremos da corda;
-
l : comprimento linear do vão;
-
d : diferença de altura entre os extremos A e B;
-
f : flecha da corda;
-
ø,B, ø A : ângulos de entrada da corda em relação a cada extremidade;
-
Y : ângulo do espaço;
-
TA, TB : tensão máxima de cada ponto.
A figura 1 mostra uma corda suspensa entre os dois pontos A e B (ancoragem a montante e a jusante da tirolesa). A configuração de equilíbrio assumida pelo cabo condutor (em negrito na figura) envolve uma certa flecha f que dependerá da quantidade de seu peso por unidade de comprimento de corda q (peso por metro de corda usada, N / m), força de pretensão exercida durante a fase de montagem e qualquer carga adicional aplicada ao cabo.
Se a flecha é muito pequena em relação à distância l entre os dois pontos de ancoragem (o único caso do objeto deste estudo), seu peso q por unidade de comprimento pode ser considerado "espalhado" em toda a projeção horizontal (Figura 2) facilitando muito os cálculos.
A figura 1 mostra uma corda suspensa entre os dois pontos A e B (ancoragem a montante e a jusante da tirolesa). A configuração de equilíbrio assumida pelo cabo condutor (em negrito na figura) envolve uma certa flecha f que dependerá da quantidade de seu peso por unidade de comprimento de corda q (peso por metro de corda usada, N / m), força de pretensão exercida durante a fase de montagem e qualquer carga adicional aplicada ao cabo.
Se a flecha é muito pequena em relação à distância l entre os dois pontos de ancoragem (o único caso do objeto deste estudo), seu peso q por unidade de comprimento pode ser considerado "espalhado" em toda a projeção horizontal (Figura 2) facilitando muito os cálculos.
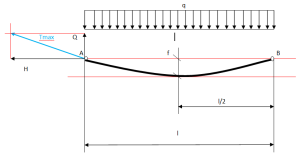
Figura 2 - Tirolesa Horizontal
É necessário dizer que o componente Q (o peso total da corda) agindo em cada ponto final será dividido em partes iguais entre os mesmos (figura 2), dado que o peso total da corda é Qtot = QXL, então teremos Q = Qtot / 2 = ( qxl) / 2 .
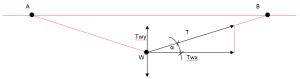
Figura 3 -
No caso da última imagem (Figura 3), destina-se a representar a decomposição das forças que atuam sobre as cordas entre os pilares das extremidades A e B como uma função da carga W aplicado em meio vão: é essencial saber e ser capaz de aplicar as fórmulas trigonométricas para cálculos que vamos fazer para poder dimensionar nosso sistema com segurança.
Para deixar isso bem claro, vamos analisar um caso hipotético de cálculo bem simples das tensões de um cabo de sustentação de carga de uma tirolesa plana com uma carga aplicada à linha central.
dados:
-
L (comprimento do teleférico): 50m
-
p (peso por m de uma corda semi-estática Petzl Axis 11mm): 82gr ---- [ie P = 8.628.6 N / m ^ 3]
-
r (resistência corda com a figura oito nó): 19KN ---- [isto é Ro.max (puxar unitária no condutor) = 200 N / mm ^ 2], [estresse Poliamidas Rendimento = 80 N / mm ^ 2], [ Alongamento elástico desta corda com limite de rendimento de cerca de 17-18%]
-
m (massa aplicada na linha central): 200 kg ---- [ie M = 1,962N]
Conhecendo as características dos equipamentos à nossa disposição e a tensão máxima possível na corda (Ro.max) antes da ruptura da mesma, que fixa um limite admissível de stress (ou carga de trabalho), de modo a não sobrecarregar o material, tendo-o para além da fase elástica (rendimento -> fase elástica). Se deram os estudos sobre a "fadiga" do material em questão são omitidos, pois são muito complexos:
Ro.amm. = Ro.max / 7 [coeff. material de segurança recomendado para materiais têxteis - Safe Working Load "SWL"] = 28,6 N / mm ^ 2
Assim que o esforço máximo permitido no sistema estiver definido, estamos prontos para prosseguir com os cálculos.??
“Durante o tensionamento de uma tirolesa, os esforços registrados em suas extremidades podem chegar a 550 daN antes da blocagem do sistema ( considerando um máximo de três pessoas puxando durante a tração, com o uso de polias sem rolamentos e bilhas). Contudo devemos sempre observar que essa tensão pode cair consideravelmente dependendo do tipo de descensor que estiver utilizando para fazer a blocagem.
Com as ancoragens dimensionadas para suportar as cordas fixadas em ambas as extremidades podemos seguir com a pré-tensão do nosso sistema, considerando que uma pessoa média utilizando um de redução sistema 5: 1, possa aplicar uma força de cerca de 250 kg.
Ao tracionar o sistema de uma tirolesa, as ancoragem são submetidas a um aumente de tensão inicial ( também chamada de tensão residual) de 80 a 120% da massa da carga. Deste modo, uma pessoa de 80 daN no centro de uma tirolesa, cuja tensão inicial era de 180 daN, implicará em esforços de 280 daN nas ancoragens, lembrando que devemos sempre levar em consideração o nosso SWL da corda recomendado pelo fabricante.
Dito isto, nosso Ro.preten. = 25,8 N / mm ^ 2
Agora vamos calcular a seta no meio do intervalo após a tensão:
f = (P x L ^ 2) / (8 x Ro.preten.) = 10 cm
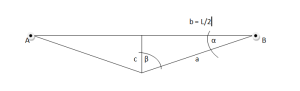
Figura 4
Na Figura 4 e retomando a Figura 3 acima, queremos mostrar como a decomposição das forças e os cálculos trigonométricos são essenciais para continuar com o dimensionamento. Calculada a flecha, agora estamos prontos para calcular o esforço adicional colocando uma carga na linha central da corda. Sabendo que uma parte do alongamento percentual foi removido com o pré-tensionamento de 250 kg e que esta corda estende-se aproximadamente 12,1% se aplicar uma carga de extremidade 440daN (ler as especificações da corda) Podemos, portanto, chegar ao comprimento aproximado dos segmentos a e c (Figura 4).
Encontrando muito pouco material que forneça uma lei exata de alongamento das cordas de acordo com o esforço, relatamos os seguintes cálculos considerados, porém, a favor da segurança:
a = inicial + 2% (acreditamos que após a pré-tensão a corda ainda tem um alongamento elástico sobre o seguinte) = 25,5 m
c = 5 m
a = 11,3º, ? = 90º-11,3º = 78,7º
Agora vamos calcular o esforço T relacionado ao segmento a:
T = M / 2sena ou M / 2cos? = 5.006.47N (5KN)
Finalmente, calculamos o esforço total atuando na âncora:
Ttot = T + Tpreten. = 5.006.47 + 2.452.5 = 7.458.97N = 7.46KN, assim teremos Ro.tot = 78.5 N / mm ^ 2> Ro.amm.
O resultado mostra-nos como o Ro.tot está bem acima do admissível, uma vez que o esforço total no condutor (760kg) é bastante considerável; com esta configuração não estamos em uma situação segura.
A noção de que "dupla segurança " é absolutamente essencial e absolutamente impossível quando operamos no campo de trabalho em altura e suspenso em cordas está implícita; diz respeito a que será necessário instalar 2 cabos de transporte com a mesma tensão quando a utilização da tirolesa se destina ao transporte de pessoas (1 ou 2) e, no caso de seções compridas que exijam pequenas setas, sistemas com três cabos pode ser adotados.

Voltando aos cálculos feitos anteriormente, vamos colocar uma segunda corda no sistema, tendo a mesma pretensão da primeira (250kg); se medíssemos agora com um dinamômetro a força existente na ancoragem após a pretensão da segunda corda, ela seria duplicada em relação a antes, ou seja, 250 kg x 2 = 500 kg. É claro que os elementos de ancoragem e o "sistema de ancoragem" devem ser à prova de bomba, dadas as altas cargas! Por outro lado, a tensão total Ttot nas cordas devido à carga aplicada na linha central é dividida entre elas e, consequentemente, também diminui a flecha na carga.
Sem isso, no entanto, ainda não estamos em condições seguras, dado que em cada corda ainda pesa cerca de 380 kg.

As soluções para o problema podem ser diferentes, como a instalação de um terceiro cabo, a redução da carga no cabo ou uma pretensão dos cabos inferiores . Se optarmos pelo último, a tensão reduzida nos condutores aumentaria a flecha f na carga e, consequentemente, diminuiria a tensão total na corda.

A fase de pré-tensão dos cabos de uma tirolesa deve ser considerada uma das mais importantes e delicadas de todo o sistema, pois influencia o resultado da tensão total que atua no sistema. Dito isto, o conselho é sempre começar com o nosso dimensionamento, colocando como Ro.tot o permissível; Desta forma, o cálculo das tensões de aplicação de uma carga e da pretensão será sempre a favor da segurança.
“Muito interessante e exaustivo o estudo conduzido por Lorenzo Contri e Stefano Secchi sobre
a excisão instantânea das cordas sob estresse: "Reconciliação instantânea de cordas sob estresse"
Então, vamos começar a partir do final dos cálculos feitos anteriormente (com uma corda):
[Ro.tot = Ro.amm. = 28,6 N / mm ^ 2 ----> Ttot = 2,718 N]
Posteriormente, vamos corrigir a seta f inicial, em vez de 10 centímetros para 50 centímetros, segue-se que o Tpret. = 512,5 N = 52,24 kg ( Ro.pret = 5,4 N / mm ^ 2)
Portanto, o esforço máximo T relativo à aplicação da carga na linha central será = Ttot - Tpret. = 2.205.5 N, o ângulo (2x ?º) no topo das minhas cordas após a aplicação da carga será de cerca de 135º e a seta final será de cerca de 9.5m.
Por fim, calculamos a carga máxima aplicável com essa configuração para permanecer segura:
T = M / 2 sen? -> M = Tx (2sen?) = 1559N = 160 kg
Se, em vez disso, quiséssemos simular a corda com o dobro da força (104,5kg), a flecha final seria de cerca de 7m e M = 95kg.
Reiteramos o conceito de dupla segurança !!! Neste caso, toda vez que eu instalar um cabo, meu sistema deve fornecer 2 cabos de sustentação; consequentemente, a vantagem será a de ter principalmente setas menores, mas também a possibilidade de aumentar a carga máxima aplicável nas cordas.

Limitando este artigo ao estudo das tensões, porém, gostaríamos ressaltar que usar nós diretamente na tensão das cordas pode ter percas consideradas, assim como o tencionamento no ID, pois a partir de 500kg de tensão, as pressão da corda no CAME bloqueia parando o seu funcionamento interno, podendo acontecer no sistema em caso de sobrecarga súbita devido a solavancos etc.
A instalação de uma tirolesa para o acesso ou para operações de resgate e evacuação exige amplo conhecimento e domínio das técnicas de trabalho em corda e recomendamos que qualquer pessoa que precise usá-lo receba treinamento adequado a esse respeito.
Ao instalar uma linha de tirolesa ou um sistema horizontal de corda estático, o ângulo formado pelos segmentos de corda quando a carga está suspensa é geralmente relativamente alto: em torno de 140º. Como vimos acima, um ângulo excessivamente aberto pode gerar importantes tensões nas ancoragens, algo que devemos evitar a todo custo quando nosso propósito é fazer uma distribuição de carga.
Agora, quando instalamos uma linha de tirolesa, o objetivo não é distribuir carga, mas mover uma carga horizontalmente.??Para fazê-lo com segurança, basta cumprir algumas regras simples:
-1. As ancoragem devem ser à prova de bombas. No caso de instalação de ancoragens tipo EN 795 A1 (o que normalmente chamamos de "chapeleta de metal", "parabolt", "química", etc.) FAÇA SEMPRE uma distribuição de cargas usando uma equalização dinâmica.
- 2. Respeite a regra de 10%: o comprimento da flecha gerada pela carga uma vez suspensa da tirolesa (sua variação em relação à horizontal) não deve ser inferior a 10% do seu comprimento total. Por exemplo, em uma tirolesa de 30 metros, a flecha gerada pela carga não deve ser menor que 3 metros. Desta forma, nos certificamos de não sobrecarregar o sistema.
- 3. As tirolesas projetadas para mover pessoas ou cargas pesadas sempre terão duas cordas paralelas com tensão similar, em alguns casos podendo aumentar o numero de cordas.
- 4. Os nós mais resistentes serão sempre escolhidos para fixar as cordas: nove, nó sem tensão, sempre ter atenção pois os nós proporciona uma perca de resistência do sistema.
Dica:
Uma dica muito útil ao calcular a força recebida pelas ancoragens de uma tirolesa é:??Carga x Comprimento / 4 x Flecha
Exemplo: Uma carga de 100kg em uma tirolesa de 40m e gerando uma flecha de 5m, obteremos: 100 x 40/4 x 5 = 200kg
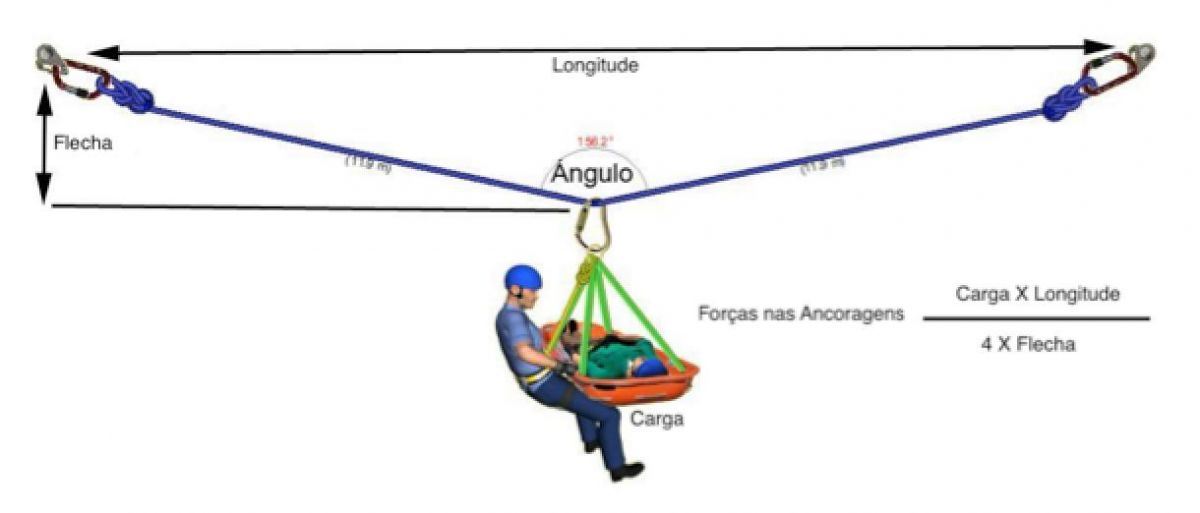
Essa dica funciona com muita precisão (margem de erro inferior a 5%) com um ângulo igual ou superior a 140 °, que são usualmente utilzados em montagens de tirolesas. Infelizmente, a margem de erro aumenta consideravelmente em ângulos menores.
Cabo de aço vs corda
Embora sempre defendemos a recomendação de não sobrecarregar a tirolesa, vale a pena esclarecer que isso é muito mais difícil de se conseguir usando cordas do que cabos de aço. Diferentes estudos mostraram que sobrecarregar uma tirolesa montada com cordas é extremamente difícil, em parte devido à elasticidade do material de que são feitas. Sob tensão, as fibras têxteis tendem a se esticar, o que tem o efeito de aumentar a flecha do sistema e, consequentemente, reduzir o ângulo de incidência. Por outro lado, os nós das cordas têm uma clara função de absorção de energia, que limita a possibilidade de sobtensão.
Aqueles que tiverem a oportunidade de tencionar uma tirolesa com a ajuda de um dinamômetro verão: assim que paramos de tencionar, a tensão que o sistema recebe cai rapidamente. No entanto, este não é o caso quando instalamos sistemas de cabo. É nulo -praticamente- a capacidade de estiramento do aço combinada com a ausência de um sistema de fixação, a mesma capacidade de absorção de energia, assim como os nós, em sistemas de cabo como base requer a máxima atenção no momento da sua construção, pois isso poderá sobrecarregar os pontos de fixação dos cabos caso não estejam bem dimensionados e instalados.
Lembramos que para tirolesas comerciais, se aplica as mesmas regras, porém temos normas específicas quanto sua construção e operação, diferente das tirolesas até aqui mencionadas, existem outros fatores nas tirolesa comerciais a serem levados em consideração, como: sistemas de freios, ação de intemperes, variação de temperatura, vento, velocidade, variação de pesos no sistema e outros fatores. Pontos a serem de observados na tirolesa de corda. Todos os cálculos demonstrados levam em conta um sistema trabalhando com equipamentos 100% adequados, levando com consideração deslocamentos de pessoas ou macas por exemplo, devemos tomar cuidado quanto as variações de tensão no sistema.
Uma descida de um socorrista com uma maca sendo debreada com trancos podem afetar diretamente nas forças envolvidas no sistema, alterando assim os cálculos e forças envolvidas, para que isso não venha acontecer, evite dar trancos ou solavancos durante o deslocamento da carga (maca, socorrista, etc...)
Outra questão a ser levado em consideração e recomendada é, o uso de sistemas debreáveis, onde cada extremidade da tirolesa é equipada com um dispositivo que permita distendê-la (nó dinâmico, descensor autoblocante ou descensor clássico). Quando possível sempre utilize sistemas de backup com fusíveis (TANDEM nó blocante), possibilitando assim um monitoramento constante e facilitando possíveis manobras como uma intervenção direta por exemplo.
Todos os cálculos demonstrados levam em conta um sistema trabalhando com equipamentos 100% adequados, levando com consideração deslocamentos de pessoas ou macas por exemplo, devemos tomar cuidado quanto as variações de tensão no sistema.
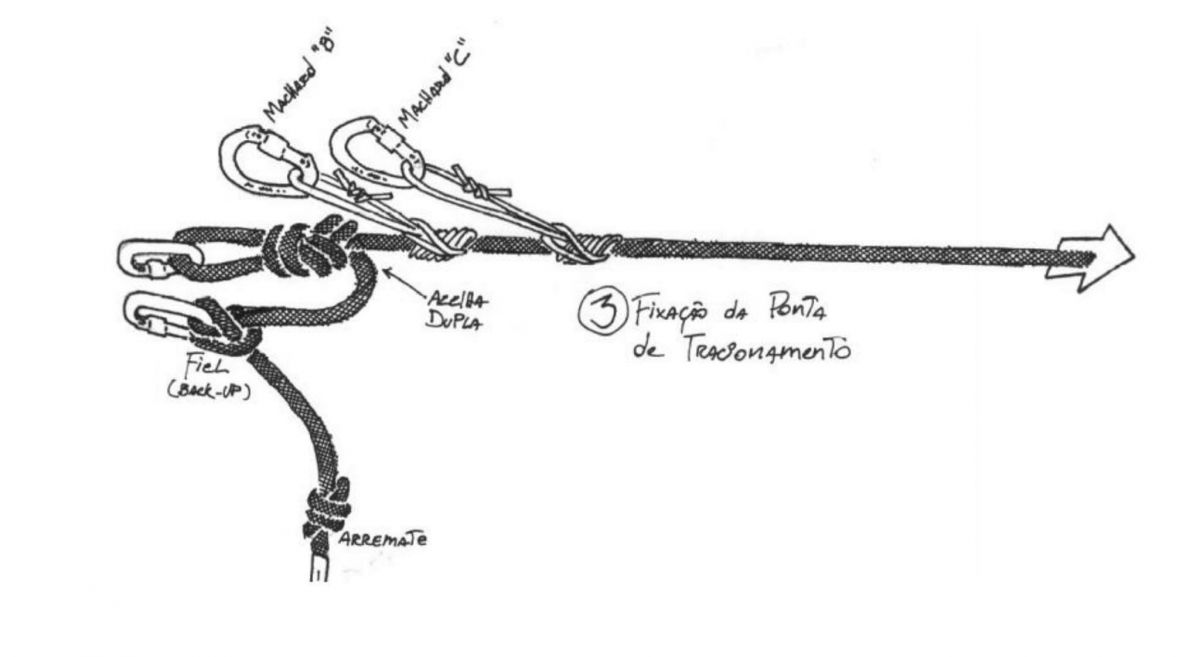
Uma dica importante sempre use o fusível abaixo do sistema debreável assim facilitará realizar manobras sem ter que move - ló do sistema, nesse caso possibilita desfazer um nó e fazer uma conexão de outra corda por exemplo, sem perder a tensão.
Boa leitura e bons estudos, espero ter contribuído com os conhecimentos aqui passados.?
Por: Maycon André Grilo
Coordenador de Projetos da empresa Guia Vertical
Especializada em montagem, projetos e execução de tirolesas.
www.guiavertical.com.br
| Fontes e referencias: Andrea De Giacometti | X-vertical Revista Low – Tech? Gran Vertical Maycon A. Grilo – Guia Vertical Manual do Epeleorresgatista – Spéleo Socurs Français Manual Treinamento de Acesso por Cordas – IRATA – N1 Prevencion y Seguridad en Trabajos Verticales – Desnivel Resgate Urbano em Altura –Denível Resgate Vertical – Eduardo José Slomp Aguiar – 1ª Edição CMC Rope Rescue Manual |
Contribuições: Gustavo Capajo : Engenheiro mecânico Matheus Baños; Fábio Souza: Diretor técnico da empresa Controle Acima Claudio Cesar Pontes: Consultor em Saúde e Segurança do Trabalho |









